Getting back into the swing of things. This is my first blog post in more than 3 years!

For this post, I’ll be using the Week 33 Tidy Tuesday dataset. This one is all about spam email.

The data consist of 4601 email items, of which 1813 items were identified as spam. This is a subset of the full dataset, with six only of the 57 explanatory variables in the complete dataset.

library(tidyverse)
library(caret)
library(corrplot)
library(tidymodels)
library(usemodels)
library(future)
library(rpart)
library(rpart.plot)
knitr::opts_chunk$set(echo = TRUE, fig.width = 4.5, fig.height = 2.5)

Load data

df <- readr::read_csv('https://raw.githubusercontent.com/rfordatascience/tidytuesday/master/data/2023/2023-08-15/spam.csv') %>%
  mutate(yesno = factor(yesno == 'y', levels=c(TRUE, FALSE)))

Data dictionary

variable    class         description
crl.tot     double        Total length of uninterrupted sequences of capitals
dollar      double        Occurrences of the dollar sign, as percent of total number of characters
bang        double        Occurrences of ‘!’, as percent of total number of characters
money       double        Occurrences of ‘money’, as percent of total number of characters
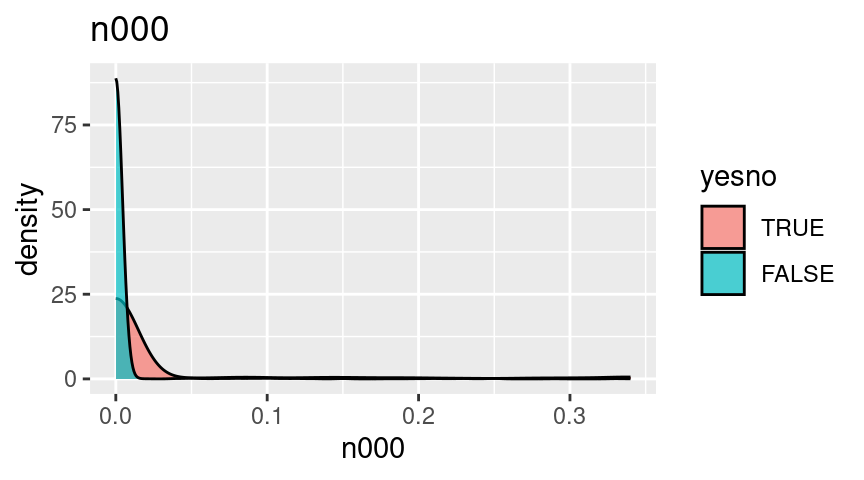
n000        double        Occurrences of the string ‘000’, as percent of total number of words
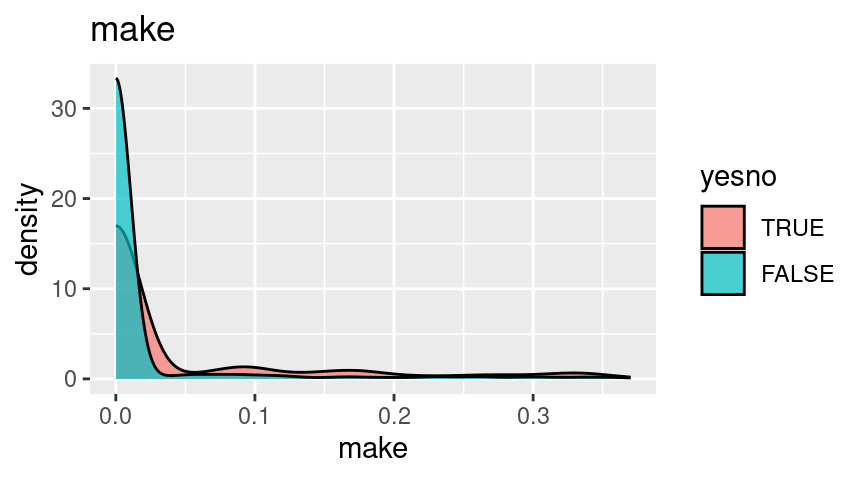
make        double        Occurrences of ‘make’, as a percent of total number of words
yesno       character     Outcome variable, a factor with levels 'n' not spam, 'y' spam

The outcome variable is yesno, a character type, and all of the other variables are of a numeric type.

We can see that a lot of the feature engineering has already been done. It seems that whoever prepared this dataset has determined that spam emails can be meaningfully identified by:

SHOUTING! (crl.tot, bang)
and talk of making money (make, money, dollar) at values of 1,000 or greater (n000)

That definitely matches my experience reading spam!

What can we do with this data?

What can we do with this data? Because this data has “ground truth” labels that tell us which emails were spam or not (yesno), and a list of features associated with each email, we can approach this as a supervised ML problem. We can use supervised ML to predict spam, to create a spam filter, for example.

Supervised ML: Predicting spam / spam filter

Average values, by spam

Let’s start by looking at some averages (mean and median), split by the outcome variable.

df %>%
  group_by(yesno) %>%
  summarise_all(mean)

# A tibble: 2 × 7
  yesno crl.tot dollar  bang  money    n000   make
  <fct>   <dbl>  <dbl> <dbl>  <dbl>   <dbl>  <dbl>
1 TRUE     471. 0.174  0.514 0.213  0.247   0.152 
2 FALSE    161. 0.0116 0.110 0.0171 0.00709 0.0735

We can see that on average, spam emails have higher mean values for each of the predictors. No surprise there.

However, the medians of some variables are zero, which suggests those variables have heavily positively skewed distributions with many zero values (sometimes called “zero-inflation”).

df %>%
  group_by(yesno) %>%
  summarise_all(median)

# A tibble: 2 × 7
  yesno crl.tot dollar  bang money  n000  make
  <fct>   <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl>
1 TRUE      194   0.08 0.331     0     0     0
2 FALSE      54   0    0         0     0     0

We can confirm this by looking at the counts of zero values, in relation to the total counts.

As we see, the vast majority of the spam emails had non-zero values on these variables, and non-spam emails had significantly fewer non-zero values, with the exception of crl.tot. In particular, spam emails were MUCH more likely to contain “!”, “$”, “000”, and “money”.

no = df %>% filter(yesno == FALSE) %>% select(-yesno)
yes = df %>% filter(yesno == TRUE) %>% select(-yesno)

round(colSums(no>0)/nrow(no)*100)

crl.tot  dollar    bang   money    n000    make 
    100      10      27       2       3      15

round(colSums(yes>0)/nrow(yes)*100)

crl.tot  dollar    bang   money    n000    make 
    100      61      83      38      33      35

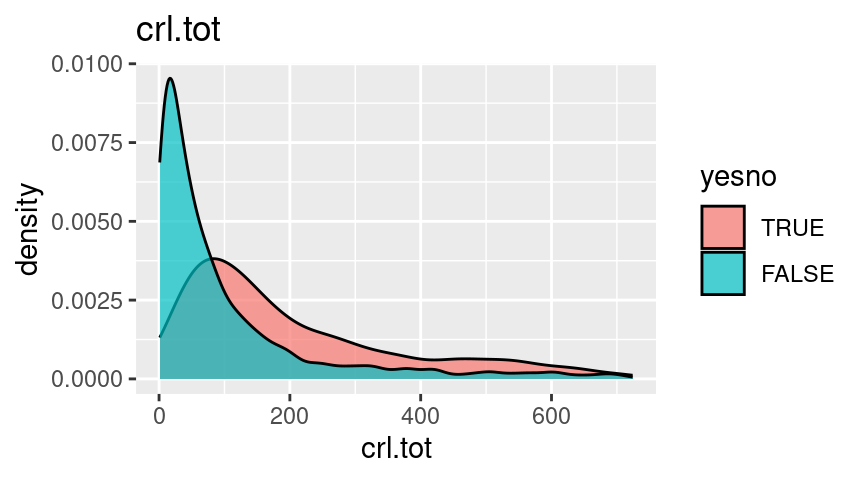
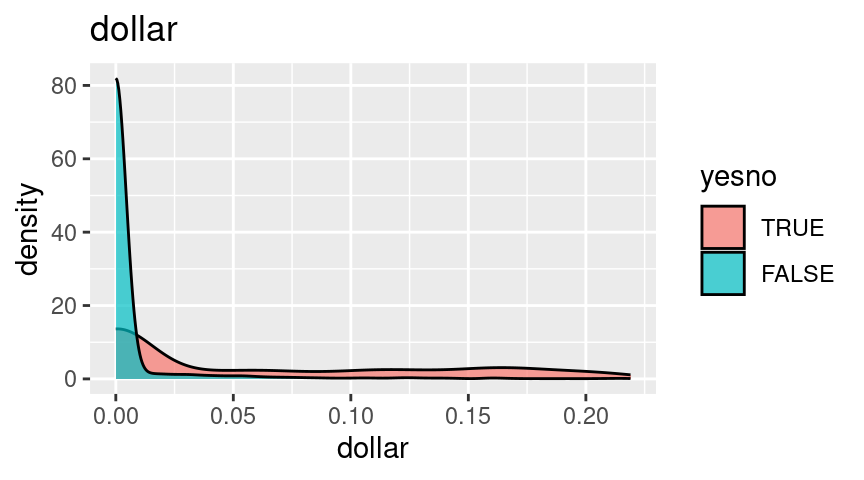
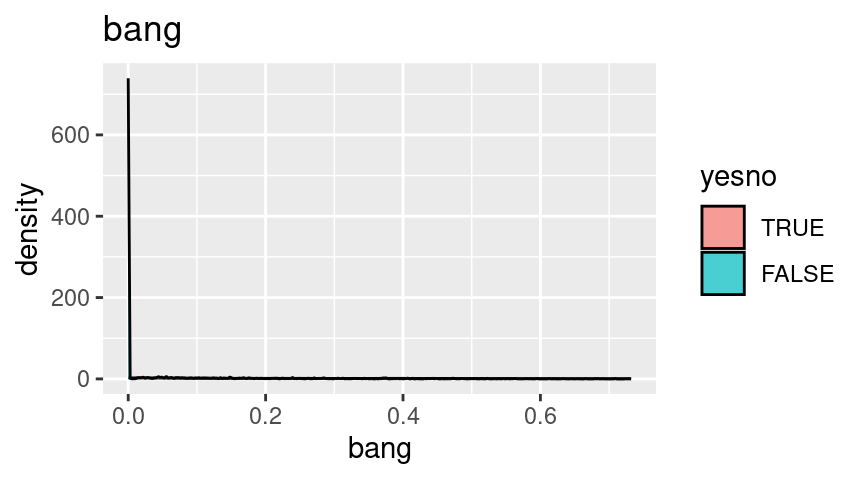
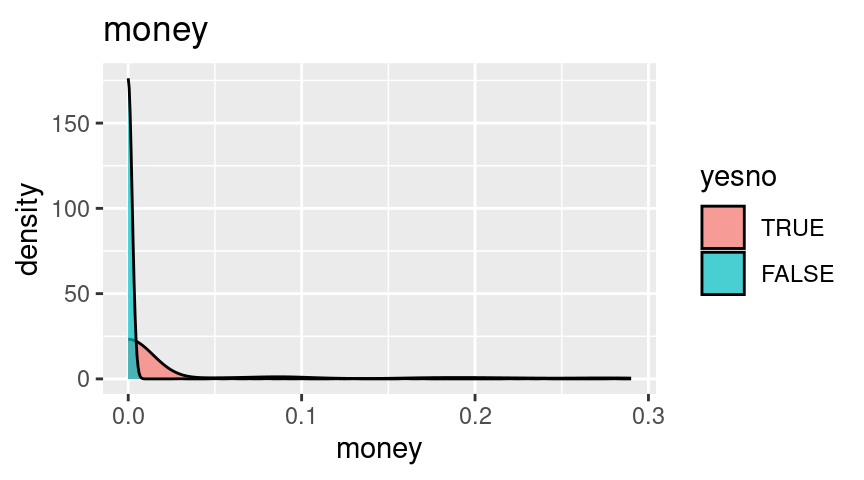
Distributions, by spam

Next, let’s look at the distributions.

For these plots, since they all have extreme skew, I’m going to truncate them at the 90th percentile and look at the left side where most of the mass is.

for (c in c('crl.tot', 'dollar', 'bang', 'money', 'n000', 'make')){
  
  qtile_90 <- quantile(df[[c]], .90)
  
  df %>%
    filter(!!sym(c) < qtile_90) %>%
    ggplot(aes(x = !!sym(c), fill=yesno)) +
      geom_density(alpha=.7) +
      ggtitle(c) -> plot
  print(plot)
  
}

Feature correlations

It doesn’t look like the features are very strongly correlated. The strongest correlation is between n000 and dollar, which is not particularly surprising since I would expect that “000” would tend to appear in the context of a dollar value like “$1000”.

df %>% 
  select(-yesno) %>%
  cor(use = "complete.obs")

           crl.tot    dollar       bang      money       n000       make
crl.tot 1.00000000 0.2019477 0.03632120 0.08099318 0.16597657 0.08916478
dollar  0.20194768 1.0000000 0.14291296 0.10469131 0.31097072 0.11741853
bang    0.03632120 0.1429130 1.00000000 0.05107591 0.07010334 0.05829200
money   0.08099318 0.1046913 0.05107591 1.00000000 0.05258693 0.18815518
n000    0.16597657 0.3109707 0.07010334 0.05258693 1.00000000 0.13407211
make    0.08916478 0.1174185 0.05829200 0.18815518 0.13407211 1.00000000

If we convert the features to boolean, we can see that the presence of features have stronger correlations. The strongest correlation is again between dollar and n000, but money and dollar also occur together more often than not.

df %>%
  select(-yesno, -crl.tot) %>%
  mutate(dollar = dollar > 0,
         bang = bang > 0,
         money = money > 0,
         n000 = n000 > 0,
         make = make > 0
  ) %>%
  cor(use = "complete.obs")

          dollar      bang     money      n000      make
dollar 1.0000000 0.3779057 0.5058803 0.5372603 0.4133374
bang   0.3779057 1.0000000 0.3290505 0.3404896 0.2641339
money  0.5058803 0.3290505 1.0000000 0.4140177 0.4092119
n000   0.5372603 0.3404896 0.4140177 1.0000000 0.3757565
make   0.4133374 0.2641339 0.4092119 0.3757565 1.0000000

Simple classification algorithm

Just for fun, let’s see how well we can distinguish spam vs. not spam using a simple heuristic.

I’ll label anything as spam if it contained at least 1 “money”, “$”, “000”, and “!” OR if it contained more than 100 uninterrupted sequences of capital letters and at least 1 “!”. This is just what comes to mind after looking at the frequency plots above.

df %>%
  mutate(simple_spam_flag = factor((money > 0 & dollar > 0 & bang > 0 & n000 > 0) | 
                                     (crl.tot > 100 & bang > 0), 
                                   levels=c(TRUE, FALSE))
         ) -> df_flag

This simple classification algorithm achieved an accuracy of 79%, with 64% sensitivity and 89% specificity. This doesn’t seem too bad. But what is a good baseline of performance?

confusionMatrix(df_flag$simple_spam_flag, df_flag$yesno, mode='everything')

Confusion Matrix and Statistics

          Reference
Prediction TRUE FALSE
     TRUE  1172   309
     FALSE  641  2479
                                          
               Accuracy : 0.7935          
                 95% CI : (0.7815, 0.8051)
    No Information Rate : 0.606           
    P-Value [Acc > NIR] : < 2.2e-16       
                                          
                  Kappa : 0.5533          
                                          
 Mcnemar's Test P-Value : < 2.2e-16       
                                          
            Sensitivity : 0.6464          
            Specificity : 0.8892          
         Pos Pred Value : 0.7914          
         Neg Pred Value : 0.7946          
              Precision : 0.7914          
                 Recall : 0.6464          
                     F1 : 0.7116          
             Prevalence : 0.3940          
         Detection Rate : 0.2547          
   Detection Prevalence : 0.3219          
      Balanced Accuracy : 0.7678          
                                          
       'Positive' Class : TRUE

We can see that the base rate of spam is 39%.

mean(df$yesno == TRUE)

[1] 0.3940448

A good baseline model might be to predict the majority class, which in this case is not-spam.

This “always predict FALSE” baseline model can be expected to achieve 1 minus the base rate of spam (i.e., 61%), and we can see that this is the case if we construct just such a model. This tells us that the heuristic model above is quite a bit better than a completely naive model.

confusionMatrix(factor(rep('FALSE',nrow(df_flag))), df_flag$yesno, mode='everything')

Warning in confusionMatrix.default(factor(rep("FALSE", nrow(df_flag))), :
Levels are not in the same order for reference and data. Refactoring data to
match.

Confusion Matrix and Statistics

          Reference
Prediction TRUE FALSE
     TRUE     0     0
     FALSE 1813  2788
                                          
               Accuracy : 0.606           
                 95% CI : (0.5917, 0.6201)
    No Information Rate : 0.606           
    P-Value [Acc > NIR] : 0.5064          
                                          
                  Kappa : 0               
                                          
 Mcnemar's Test P-Value : <2e-16          
                                          
            Sensitivity : 0.000           
            Specificity : 1.000           
         Pos Pred Value :   NaN           
         Neg Pred Value : 0.606           
              Precision :    NA           
                 Recall : 0.000           
                     F1 :    NA           
             Prevalence : 0.394           
         Detection Rate : 0.000           
   Detection Prevalence : 0.000           
      Balanced Accuracy : 0.500           
                                          
       'Positive' Class : TRUE

Decision Tree

Proceeding from simpler to more complex, we can go a step further and try fitting a decision tree model. The decision tree will help us to identify a more sophisticated rule set for classifying spam mail. Decision trees also have the advantage of being highly interpretable.

We’ll start by splitting our data into training and test – that way, we won’t be testing performance on the same data that our model was trained on, and we can minimize the risk of overfitting.

set.seed(200)
split <- initial_split(df)
train <- training(split)
test <- testing(split)

Next, we’ll fit the model and then visualize its logic.

We can read this chart by starting at the root node and following the branches until we reach a terminal node. The predicted value at this terminal node will give us the prediction that the model has made, and the path that we followed to get there provides its reasoning for the prediction.

So for example, if we follow the tree to the left-most terminal node, we can see that it would predict that an email was spam if it contained dollar >= 0.056. If we follow the tree to the right-most terminal, we can see that it would predict that an email was not spam if it contained dollar < 0.056 and bang >= 0.12. The percentage value in the node tells us what percentage of emails met these criteria. So 24% of emails met the former criteria, and 54% the latter.

decision_tree <- rpart(yesno ~ ., data=train, method='class')
decision_tree

n= 3450 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

 1) root 3450 1358 FALSE (0.3936232 0.6063768)  
   2) dollar>=0.0555 839   94 TRUE (0.8879619 0.1120381) *
   3) dollar< 0.0555 2611  613 FALSE (0.2347759 0.7652241)  
     6) bang>=0.1205 739  330 TRUE (0.5534506 0.4465494)  
      12) crl.tot>=80.5 361   75 TRUE (0.7922438 0.2077562) *
      13) crl.tot< 80.5 378  123 FALSE (0.3253968 0.6746032)  
        26) bang>=0.802 85   34 TRUE (0.6000000 0.4000000) *
        27) bang< 0.802 293   72 FALSE (0.2457338 0.7542662) *
     7) bang< 0.1205 1872  204 FALSE (0.1089744 0.8910256) *

rpart.plot(decision_tree)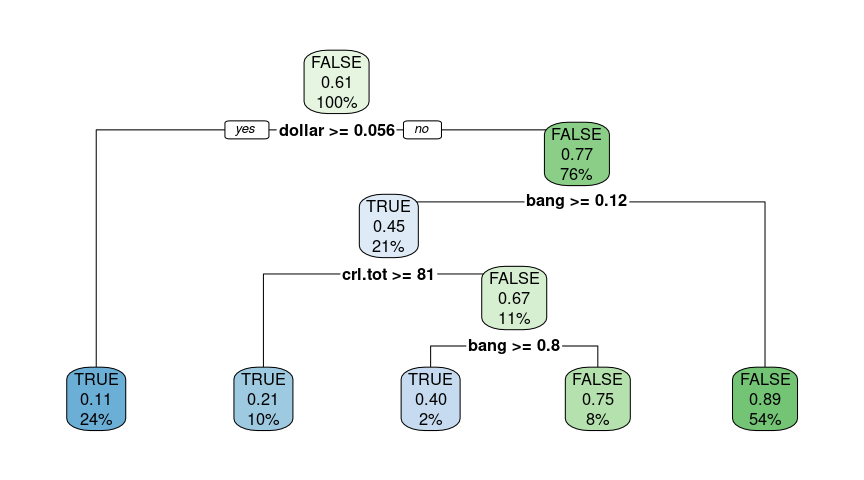

Finally, we can test the model on the out-of-sample test dataset and see how it performs.

Overall it achieved an accuracy of 85%, with 78% sensitivity and 89% specificity. This model has similar specificity as the heuristic model, but better sensitivity, and therefore better overall accuracy.

test_pred <- predict(decision_tree, test, type='class')
confusionMatrix(test_pred, test$yesno, mode='everything')

Confusion Matrix and Statistics

          Reference
Prediction TRUE FALSE
     TRUE   355    77
     FALSE  100   619
                                          
               Accuracy : 0.8462          
                 95% CI : (0.8241, 0.8666)
    No Information Rate : 0.6047          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.6755          
                                          
 Mcnemar's Test P-Value : 0.0982          
                                          
            Sensitivity : 0.7802          
            Specificity : 0.8894          
         Pos Pred Value : 0.8218          
         Neg Pred Value : 0.8609          
              Precision : 0.8218          
                 Recall : 0.7802          
                     F1 : 0.8005          
             Prevalence : 0.3953          
         Detection Rate : 0.3084          
   Detection Prevalence : 0.3753          
      Balanced Accuracy : 0.8348          
                                          
       'Positive' Class : TRUE

Random forest

Next, we’ll try a random forest model. Random forest models tend to perform better than decision trees, due to the fact that they are ensemble decision trees, meaning they group together the decisions of lots of decision trees. But as a result, they tend to be less interpretable. So if our goal was only to create the most accurate prediction model possible, then a random forest would be better suited to the task.

cv <- vfold_cv(train)

I’ll use usemodels::use_ranger to give me a starting template.

use_ranger(yesno ~ ., train)

ranger_recipe <- 
  recipe(formula = yesno ~ ., data = train) 

ranger_spec <- 
  rand_forest(mtry = tune(), min_n = tune(), trees = 1000) %>% 
  set_mode("classification") %>% 
  set_engine("ranger") 

ranger_workflow <- 
  workflow() %>% 
  add_recipe(ranger_recipe) %>% 
  add_model(ranger_spec) 

set.seed(17214)
ranger_tune <-
  tune_grid(ranger_workflow, resamples = stop("add your rsample object"), grid = stop("add number of candidate points"))

I’ll remove the parameter tuning to keep things simple.

ranger_recipe <- 
  recipe(formula = yesno ~ ., data = df)

ranger_spec <- 
  rand_forest(trees = 1000) %>% 
  set_mode("classification") %>% 
  set_engine("ranger") 

ranger_workflow <- 
  workflow() %>% 
  add_recipe(ranger_recipe) %>% 
  add_model(ranger_spec)

Next, I’ll fit the model using a resampling approach.

set.seed(100)
plan(multisession)

fit_rf <- fit_resamples(
  ranger_workflow,
  cv,
  metrics = metric_set(accuracy, sens, spec),
  control = control_resamples(verbose = TRUE,
                              save_pred = TRUE,
                              extract = function(x) x)
)

Overall, accuracy is pretty good: 89% accuracy, 79% sensitivity, and 95% specificity.

fit_rf %>%
  collect_metrics()

# A tibble: 3 × 6
  .metric  .estimator  mean     n std_err .config             
  <chr>    <chr>      <dbl> <int>   <dbl> <chr>               
1 accuracy binary     0.886    10 0.00497 Preprocessor1_Model1
2 sens     binary     0.793    10 0.00797 Preprocessor1_Model1
3 spec     binary     0.946    10 0.00523 Preprocessor1_Model1

Next, we can check the performance on the test set.

We can use collect_metrics() function on the last fit.

ranger_workflow %>%
  last_fit(split) %>% 
  collect_metrics()

# A tibble: 2 × 4
  .metric  .estimator .estimate .config             
  <chr>    <chr>          <dbl> <chr>               
1 accuracy binary         0.888 Preprocessor1_Model1
2 roc_auc  binary         0.930 Preprocessor1_Model1

Or we can use confusionMatrix() to get a bit more information.

Performance on the test set is similar to the training performance. Overall, accuracy is pretty good – and better than the decision tree. For a spam detection filter, we’d want to bias towards minimizing false positives (it would arguably be worse for people to lose legitimate mail to the filter, than to have spam mail slip through), and here we see that the specificity was quite good at ~95%.

ranger_workflow %>%
  last_fit(split) %>% 
  extract_workflow() -> final_model

confusionMatrix(predict(final_model, test)$.pred_class, test$yesno, mode='everything', positive='TRUE')

Confusion Matrix and Statistics

          Reference
Prediction TRUE FALSE
     TRUE   362    34
     FALSE   93   662
                                          
               Accuracy : 0.8897          
                 95% CI : (0.8701, 0.9072)
    No Information Rate : 0.6047          
    P-Value [Acc > NIR] : < 2.2e-16       
                                          
                  Kappa : 0.7639          
                                          
 Mcnemar's Test P-Value : 2.652e-07       
                                          
            Sensitivity : 0.7956          
            Specificity : 0.9511          
         Pos Pred Value : 0.9141          
         Neg Pred Value : 0.8768          
              Precision : 0.9141          
                 Recall : 0.7956          
                     F1 : 0.8508          
             Prevalence : 0.3953          
         Detection Rate : 0.3145          
   Detection Prevalence : 0.3440          
      Balanced Accuracy : 0.8734          
                                          
       'Positive' Class : TRUE